The Hoek Experiment (1868) by Doug Marett (2010) Martinus Hoek performed an experiment in 1868 attempting to see if it is possible to detect the movement of the earth using an interferometer where the index of refraction of the light paths is different in the different arms. The interferometer can be understood using Fig. 1: 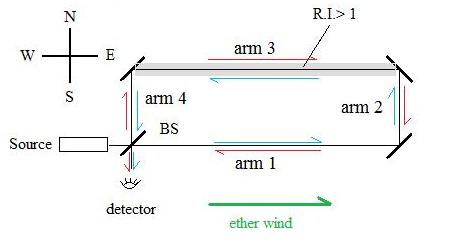
Light leaves the source and is split into two paths at the beam-splitter BS. The blue light path goes along arm 1 to 2 to 3 to 4 and then exits at the detector. The red light path goes along arm 4 to 3 to 2 to 1 and then exits at the detector. The two beams are made to interfere at the detector, and any shift in the interference pattern would reveal a difference in the propagation time between the two paths. All of the arms are in air, except for arm 3, which is in water, which has an index of refraction of 1.333. If we consider the expected speed of light from classical Galilean addition of velocities, and assuming a preferred frame for light (a medium in which the speed of light is constant, such as an ether ) moving in the direction of the arrow, the time for light to travel each path would be:
Where: L = length of each arm , c = speed of light in preferred frame , v = velocity of preferred frame n = refractive index of water = 1.333 Arm 3 lies on the W to E line of the compass.
If the device is then rotated 90 degrees so that arm 3 now lies N-S, we would get:
After adding all these time quantities in each direction, and subtracting the W-E orientation time difference from the N-S orientation time difference, we get the expected fringe shift from one orientation to another. This calculation can be seen in the interactive Hoek Webapp provided on this site. If we assume all arm lengths are one meter, and the velocity of the preferred frame is the velocity of the earth in its orbit around the sun of 30 km/s, then the expected time difference would be: Dt = 5.18 E -13 seconds so the expected fringe shift between the two beams would be: Dt* c / l = 246 fringes. However, Hoek did not see any fringe shifts at all. See his original Hoek paper in English here. Hoek decided that there must be some factor j, such as a dragging of the ether by the earth as it moves through space, that was obscuring the expected fringe shift. If j = 0 then there would be no ether drag, and if j = 1 then there would be full ether drag. This was re-expressed as follows: Arm 3 in line W to E.
If the device is then rotated 90 degrees so that arm 3 now lies N-S, we would get:
Arm 1 Arm 2 Arm 3 Arm 4 Blue path L1 / c L2 / (c - v + j) L3 / (c/n) L4 / (c +v - j) Red path L1 / c L2 / (c + v - j) L3 / (c/n) L4 / (c - v + j)
The value of j that exactly resulted in a null result for the experiment was: j = v(1-1/n2)
where: v = velocity of ether experienced by each arm, n = refractive index of arm. This value for j was the well known Fresnel Drag coefficient. Does the experimental result of Hoek demonstrate that there must be a partial ether drag as assumed by Fresnel? This problem was taken up by Hendrick Lorentz in the late 1800's. Lorentz wanted to account for the results of all first-order interferometer experiments (such as Hoek's) which involved the Fresnel drag coefficient. Lorentz succeeded in deriving this coefficient from his version of EM theory in 1892 (3), his first extensive work on the electrodynamics of moving bodies. His equations governed the propagation of EM waves in a moving frame of reference (the dielectric) which itself was moving through a preferred frame (the ether). He found that an EM wave propagating along a dielectric, where the dielectric has a velocity v with respect to the ether, would mean that the speed of light in the dielectric (c') becomes c' = c/n - v/n2. Written another way, the velocity of the light with respect to the ether becomes:
c' = c/n - v/n2 +v = c/n + [ v(1-1/n2) ]
the value in the square brackets is the Fresnel Drag coefficient. This new understanding meant that it is the light being dragged by the dielectric medium and not the ether which is responsible for the null result. It was Lorentz's accomplishment in explaining why no interferometer experiment could be successful in detecting an ether, that made it convenient for some to do away with the ether altogether. What cannot be detected does not exist, or at least that was the attitude taken by Einstein when he used Lorentz's theorem of corresponding states, now re-named by Poincare the "Lorentz transformations" and incorporated them into his new theory of special relativity. What should be taken from this however is that the modern interpretations of these experiments implies only that if an ether as conceived of by Lorentz does exist, the result of a first order experiment such as Hoek's will always yield a null result, just as would a prediction by special relativity, which is based on the same Lorentz transformations. The existence or non-existence of a medium of space or a preferred frame for light would require a different experiment, perhaps one that has not yet been conceived of. Until then, the theory of choice become a matter of a researchers personal preference. To quote Mansouri and Sexl (4): First order tests cannot be used to distinguish between special relativity and ether theories, as has sometimes been stated. No such "experimentum crusis" is possible in principle, since the two classes of theories can be transformed into one another by a change of conventions about clock synchronization." References: 1) Martinus
Hoek, (1868) Determination
of the Speed with which a Light Wave is Entrained Crossing a Moving
Medium 2)
Interactive Hoek Interferometer Simulator. http://www.conspiracyoflight.com/Hoekwebapp/Hoek.htm
3) Lorentz, H. (1892) “La theorie electromagnétique de Maxwell et son application aux corps mouvants.” Archives néerlandaises des sciences exactes et naturelles 25 (1892): 363–552. 4) Mansouri, Reza, Sexl, Roman, "A Test Theory of Special Relativity: II First Order Tests. " General Relativity and Gravitation, Vol. 8, No.7 (1977) p. 515-524.
|